ユークリッドの互除法はなぜ成り立つ？分かりやすく解説。

生徒からこんな質問を受けました。

「ユークリッドの互除法ってなんで成り立つんですか」と。

今回はユークリッドの証明について分かりやすく解説していきたいと思います！

ユークリッドの互除法とは

まずユークリッドの互除法とは、

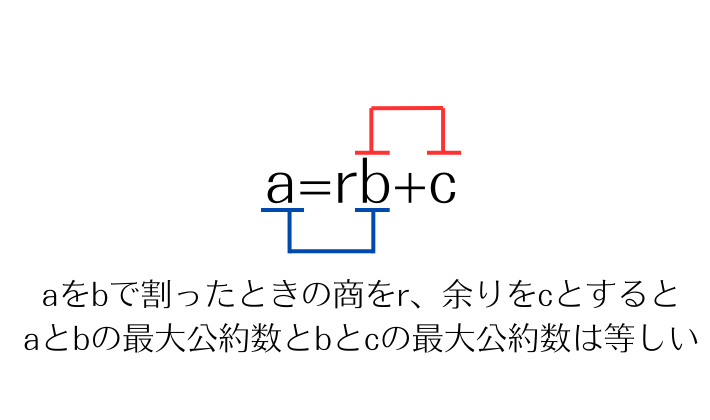
こういうことでした。

ではなぜこれが成り立つのか知りたいという向上心の塊の人向けに解説を挟みながら証明していきます！

実際に証明してみた

a=rb+c　（a,b,c,rは整数）とします。

このとき、aとbの最大公約数をG₁、bとcの最大公約数をG₂とします。

この証明のゴールはG₁=G₂ということを念頭においておきましょう。

まず、aとbの最大公約数がG₁から

a=G₁a’

b=G₁b’（a’,b’は互いに素）と表せます。

aとbの共通しているところがG₁に集まって、被りのない残りかすがa’とb’に入っているイメージです。だからa’とb’は互いに素です。

これを元の式に代入すると、

G₁a’=rG₁b’+c

rG₁b’を移行して整理すると

c=G₁(a’-rb’)

となりました。

a’-rb’は整数なのでG₁というのはcの約数でもあることが分かりました。

よって、G₁はbの約数でもありcの約数でもあるのでbとcの公約数です。

しかし、bとcの最大公約数はG₂なので

G₁≦G₂…①

これと同じことをもう一度します。

b=G₂b’’

c=G₂c’’（b’’とc’’は互いに素）

元の式に代入して、

a=rG₂b’’+G₂c’’

  =G₂(rb’’+c’’)

よってrb’’+c’’は整数より、G₂はaとbの公約数。

aとbの最大公約数はG₁より、

G₁≧G₂…②

よって①と②から、

G₁はG₂以上かつG₂はG₁以上なので

それすなわちG₁=G₂となるわけです。

まとめ

問題集をやっているとユークリッドの互除法を使う問題が多くあります。

どんな定理も、まずは使いこなすことが大事ですが、なぜこれが成り立つのかということに着目していくことが結局のところ数学力向上の近道です！！

難関大になれば定理の証明を出してくる大学もあるのでこの際互除法の証明は身につけておきましょう！

たいよう

私を３つの単語で表すとすれば、 京大生、テニスプレイヤー、チェリーボーイ。